[ad_1]
In the process of studying the possibility of developing processes of self-organization of subsystems of the second level in TS of diesel engine, theories of thermodynamics of non-stationary processes, solid state physics, wear theory and the fundamentals of mechanics were used. To solve the differential equation of the energy-mass transfer, a numerical calculation technique was used.
The object of research is the processes of the self-organization of subsystems of the second level in TS of diesel engine.
The subject of research is the criterion of development of processes of the self-organization of subsystems of the second level in TS of diesel engine.
Research hypothesis is based on the Glansdorff–Prigozhin criterion and the use of dependencies that combine the physical, mechanical and tribological properties of the TS, the criterion of development of processes of the self-organization of subsystems of the second level in TS of diesel engine can be obtained.
For the numerical solution of the differential equation of the energy-mass transfer, a personal computer and the corresponding software were used.
Data for research
TS of diesel engines—it is the set of physical objects that interact with each other by contact-mechanical means, and at the contact points occurs the breakage of linear velocities of the interacting objects, where the mutual energy-mass transfer takes place20.
The simple TS of diesel engines consist of two facilities that operate without lubricating surface with dry abrasive mass. First of all, this concerns the operation of diesel vehicles during the start-up period, and especially at low temperatures. Secondly, even in the presence of lubrication, a regime without lubrication of the surface with dry abrasive mass is possible.
The complex TS of diesel engines are complemented by the active environment, lubricant-coolants and artificially introduced energy sources. In turn, any system is divided into subsystems of the highest order.
The operation of subsystems of diesel engines of any level can be described by the equation of the energy balance and the kinetics of the components that are included in present subsystem and define the nature of the interaction, the internal structural and energy state. In consequence of the interaction between the components of the subsystems in TS of diesel engines, their energy is spent on changing the character of behavior, and another—on changing their internal state21. The latter is the energy that is expended to change the kinetics of the interaction between the components of the subsystems in TS of diesel engines and it is the major component of energy balance of the subsystems of the next higher level. The subsystems of each level are characterized by their most informative energy parameters in absolute, specific, gradient and other ratios. Hereafter, they are used to describe the energy, balance and kinetic relations that show the first and the second law of thermodynamics3. The combination of the energy relations of functioning of subsystems of different levels is possible, but impractical in the presence of variables of different orders in one equation. Therefore, each subsystem independently from its level should be described by its thermodynamic relation. The lower-level subsystems are described by the equation of energy balance in absolute values or their streams. It is appropriate to describe the high-level subsystems by energy flux density, and the subsystem of higher orders—by specific energy parameters or their gradient expressions.
The hierarchy of subsystems of three levels in TS of diesel engines is presented graphically in Fig. 1.
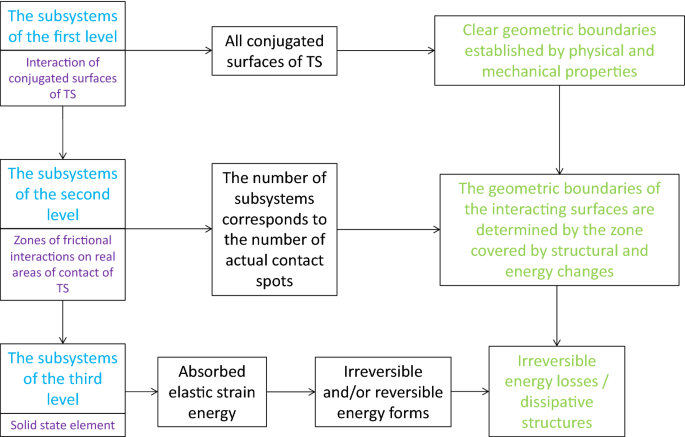
The hierarchy of subsystems of three levels in TS of diesel engines.
In considering the processes of friction and wear that occur in diesel engines, the subsystems of the first level may include the interaction of connected parts with identified geometric borders, different physical and mechanical properties, with the known laws of the external load and movement of each point, as well as the specified interval of velocities in the TS of diesel engines.
The subsystems of the second level in the TS of diesel engines may include areas of friction interactions on the real areas of contact. The number of subsystems of the second level corresponds to the number of spots of actual contact. Geometric boundaries of the interacting objects of present subsystems are defined by the zone, in which the structural and energetic changes are observed.
The subsystem of the third level in the TS of diesel engines may include micro-volume of contact and subcontact zones, covered by the structural and energy changes of triboprocess. In contrast to the subsystems of the first and the second levels in the TS of diesel engines, which provide for interaction, at least of two solid-phase objects, the components of subsystems of the third order is the one solid-phase formation, the change of the structure of which is due to its penetrating flow of energy and matter1.
The development of the self-organizing systems is determined by the Glansdorff-Prigogine criterion3, under which in any unbalanced system the rate of change of entropy production decreases. Stationary or stable thermodynamic processes are characterized by minimum entropy production.
The energy balance equation for the subsystems of the first level is presented in absolute energy values or in their flows3:
$$ \overline{F} \cdot \overline{{V_{\kappa } }} = \frac{d}{dt}(Q + W_{m} ) = \dot{Q} + \dot{E}_{m} , $$
(1)
where \(\overline{F}\) is the average force of contact interaction in the TS; \(\overline{{V_{\kappa } }}\) is the average sliding velocity; \(Q\) is the amount of heat that stood out in the process of contact interaction between elements of the TS; \(W_{m}\) is the mechanical component of the energy balance of the TS; \(\dot{Q}\) is the heat flow; \(\dot{E}_{m}\) is the flow of mechanical energy in the TS of diesel engines.
The mechanical component of the energy balance of the TS of diesel engines describes the energy cost for surface structural changes and their wear. Its part does not exceed (1.5–3.0) % of the work of friction, thus:
$$ \overline{F} \cdot \overline{{V_{\kappa } }} \approx \dot{Q}. $$
(2)
This equation shows the balance between work of friction and released thermal energy in the TS of diesel engines or the process of dissipation of the input mechanical energy.
The increase of the produced entropy \(\Delta \,S\) determines the mode of operation of the TS of diesel engines. The break-in period is characterized by the lowering of \(\Delta \,S\), the steady-state—by its stabilization, and catastrophic wear—by its dramatic growth.
Thermodynamics of the subsystems of the second level in the TS of diesel engines considers the balance relationships, which reflect the transformation of the nondissipative mechanical energy, which can be written as3:
$$ \frac{{\partial^{2} E_{m} }}{\partial m\partial t} = \frac{{\partial^{2} U}}{\partial m\partial t} + \frac{{\partial^{2} A_{wp} }}{\partial m\partial t} + \frac{{\partial^{2} Q}}{\partial m\partial t} $$
(3)
where \(U\) is the internal energy; \(A_{wp}\) is the work of the wear process; \(m\) is the mass of the objects of the contact interaction.
The process of absorption of the elastic internal energy by the contact layers of the TS of diesel engines takes place at the initial moment of frictional interaction or at the break-in period23. Upon completion of this process, its intensity drops to zero, periodically renewing as the new contact layers open due to wear.
Consequently, in the steady process of friction, the energy costs for the formation of secondary structures become the values of lower order than the remaining terms of Eq. (3). Then the energy balance equation of the subsystem of the second level in the steady process of wear will look like:
$$ \frac{{\partial^{2} E_{m} }}{\partial m\partial t} = \frac{{\partial^{2} U}}{\partial m\partial t} + \frac{{\partial^{2} Q}}{\partial m\partial t}. $$
(4)
If the entropy is taken into account in the expression (3), or rather the second variation of the entropy (the excess entropy production)24, we would obtain the expression, which is the criterion of possibility of development of processes of the self-organization of subsystems of the second level:
$$ \frac{{\partial^{2}_{m} }}{\partial m\partial t} = 2\frac{{\partial^{2} A_{wp} }}{\partial m\partial t} – \left( {\frac{\partial I}{{\partial V}}V + I} \right)^{2} \left( {\delta V} \right)^{2} \frac{{n^{2} }}{{D\,T_{c} }} + \frac{{^{2} }}{{T^{2} B\lambda }}\left( {\frac{\partial \mu }{{\partial v}}v + f} \right)^{2} \left( {\delta V} \right)^{2} – Tgrad\frac{\rho }{T}\left( {\left( {\frac{\partial }{\partial t}\left( {\delta \rho_{g} + \delta v_{gs} } \right)} \right)^{2} + \rho_{g} v_{gs} } \right), \quad \quad \frac{{\partial E_{m} }}{\partial m} \le 0,\;\;\;\frac{{\partial E_{m} }}{\partial t} \le 0, $$
(5)
where \(T_{c}\) is the cooling temperature of the surface of the part; \(T\) is the absolute temperature; \(\mu\) is the chemical potentials; \(\rho\) is the potential of the dislocation density; \(\lambda\) is the thermal conductivity; \(f\) is the coefficient of friction; P is the pressing force at the contact; \(n = \partial N/\partial V\) is the volume concentration of particles; \(\partial V\) is the infinitesimal volume; \(I\) is the intensity wear; \(v\) is the sliding velocity; \(D\) is the quasidiffusion coefficient; \(B\) is the height of microasperities; \(\rho_{g}\) is the average volume density of mobile dislocations; \(v_{gs}\) is the average sliding velocity of mobile dislocations.
The criterion for the possibility of development of processes of the self-organization of subsystems of the second level (5) shows that in a real irreversible process there is a decrease in the flow of mechanical energy.
The pressing force at the contact, for example, for the TS of diesel engine “crankshaft-insert” can be defined:
$$ P = \left( {P_{g} – \left( {m_{p} + m_{1} + m_{2} \cdot \frac{{l_{c} }}{l}} \right) \cdot j – F_{wp} } \right), $$
(6)
where \(P_{g}\) is the force of gas pressure on the piston acting along the axis of the cylinder; \(m_{p}\), \(m_{1}\), \(m_{2}\) are the mass of the piston, the connecting rod, which moves back and forth along the axis of the cylinder and the mass of the connecting rod, attributed to its center of mass, which performs a complex movement, respectively; \(l\), \(l_{c}\) are the total length of the connecting rod and the distance from the center of mass to its upper head, respectively; \(j\) is the acceleration of reciprocating motion of the piston; \(F_{wp}\) is the force of the wear process in TS of diesel engine.
As a result, expression (5) will take the form:
$$ \frac{{\partial^{2} E_{m} }}{\partial m\partial t} = 2\frac{{\partial^{2} A_{wp} }}{\partial m\partial t} – \left( {\frac{\partial I}{{\partial V}}V + I} \right)^{2} \left( {\delta V} \right)^{2} \frac{{n^{2} }}{{DT_{c} }} + \left( {P_{g} – \left( {m_{p} + m_{1} + m_{2} \cdot \frac{{l_{c} }}{l}} \right) \cdot j – F_{wp} } \right)^{2} \left( {\frac{\partial \mu }{{\partial v}} v + f} \right)^{2} \frac{{\left( {\delta V} \right)^{2} }}{{T^{2} B\lambda }} – Tgrad\frac{\rho }{T}\left( {\left( {\frac{\partial }{\partial t}\left( {\delta \rho_{g} + \delta v_{gs} } \right)} \right)^{2} + \rho_{g} v_{gs} } \right),\frac{{\partial E_{m} }}{\partial m} \le 0,\;\;\;\frac{{\partial E_{m} }}{\partial t} \le 0, $$
(7)
The external manifestation of the self-organization in the subsystems of the second level is the stabilization of the wear rate, which is determined at the very end after complete stabilization of all the power, thermal and micro-geometrical parameters of the TS of diesel engines.
Thermodynamics of the subsystems of the second level shows the process of transformation of non-thermal component of external flow of mechanical energy into irreversible energy losses and the internal structure and energy transformations that occur in the contact layers at friction.
All the summed up mechanical energy is absorbed by the surface layers of friction bodies in the form of elastic strain energy. As a result, interacting structures correspond to an unbalanced condition.
All possible forms of energy can be divided into two types: reversible and irreversible3. Irreversible are those types of forms of energy, which in their development have reached the state at which their subsequent transformation into other forms is potentially impossible. They cannot be involved in the processes of transformation of structures and completely leave the subsystem by spreading in the environment. These species include thermal, acoustic and light energy. Irreversible energy forms are dominant in all tribotechnical and deformation processes.
The ongoing energy-mass transfer within the subsystems of the second level is driven by gradients of temperature, stress, chemical potentials and dislocation density. The direction of the energy-mass transfer is opposite to the vector of gradient of chemical potential, so the decrease in its intensity occurs in the course of the development of the process.
We write the boundary conditions for the differential Eq. (7) in the following form:
$$ V = V_{0} ,\;\;m = m_{0} ,\;\;\left. {\left( {\frac{\partial I}{{\partial V}}V + I} \right)^{2} \left( {\delta V} \right)^{2} } \right|_{I = 0} = 0,\;\;\;\left. {\left( {\frac{\partial \mu }{{\partial v}}v + f} \right)^{2} } \right|_{\mu = 0} = 0,\;\;\left. {\frac{{\partial A_{wp} }}{\partial t}} \right|_{t = 0} = 0,\;\;\left. {\left( {\frac{\partial }{\partial t}\left( {\delta \rho_{g} + \delta v_{gs} } \right)} \right)^{2} } \right|_{t = 0} = 0. $$
(8)
[ad_2]
Source link
